
高校生
数学の勉強法
中学の頃は数学が得意だった人でも、一筋縄でいかないのが高校数学です。 特に東大など偏差値の高い理系学部を目指す人や、医学部医学科を目指す人は、数学の試験成績が合格不合格を左右するといっても過言ではありません。 ただ、他の教科も学習内容がどんどん難しくなる中で、数学ばかりに時間を掛けているわけにもいかないので、少しでも短時間で数学の学力を身に付けたいところです。
①共通テストマーク式数学と2次記述式数学。どっちの対策に力を入れるべき?

共通テストの数学はマーク式なので、答えのみをマークするという形式の試験です。 マーク式数学においては、途中式がどれだけ立派なものでも最後の答えを間違ってしまうとその問題は0点なので、正確な計算力が求められます。 計算ミスを防ぐために、日頃から見直しをする癖を付けておきたいです。 ただ、共通テストの試験時間が70分と短いので、正確さだけでなく素早い計算力も必要です。
国立大学の二次試験や、私立大学の一般入試における数学は、記述式の試験である場合が多いです。 (一部の大学・学部においては、マーク式を採用しているところや、記述式ではあるけど答えのみを書き入れる空所補充型の形式を採っているところもあります。) 記述式数学においては、答えが合っているだけでなく、途中の式が正しく書けているかどうかも採点基準となります。 普段、数学の練習問題を解く際に途中式をちゃんと書かない人もいますが、必ず途中式も書くようにしましょう。 採点する人が読みやすく、論理性のある筋が通った式を書くように意識しましょう。 どのような途中式を書けば良いか分からないという人は、問題集の解説部分を参考にすると良いでしょう。
さて、『共通テスト→2次で記述式数学を受験予定』だという人はマーク式数学と記述式数学のどちらの対策に力を入れるべきかというと、記述式の方に力を注ぐべきです。 さすがに共通テスト直前の12月以降は、共通テスト過去問を反復するなどマーク式対策に集中すれば良いのですが、もっと早い時期から共通テスト対策に時間を掛けすぎるのは危険です。
やはり記述式の数学の方が対策に時間を要するので、記述式数学の勉強を軸にしながら時折マーク式に特化した勉強も取り入れるというスタンスでいきましょう。 マーク式ばかりを対策してきた人がいきなり記述式に対応するのは難しいですが、記述式中心に対策してきた人がいきなりマーク式に対応するのは特に難しくありません。
②理系数学と文系数学の違いは?それぞれの範囲を確認しておこう

理系数学とは「数学Ⅰ数学Ⅱ、数学A、数学B、数学C」の範囲を指します。 文系数学とは「数学Ⅱ数学Ⅱ、数学A、数学B」の範囲を指します。 よって理系数学と文系数学の違いは、数学Cが含まれるかどうかです。
大学入試の際に、大学によっては上記の範囲に対して更なる指定を設けることがあります。
志望校が決まっている人は必ず一般入試要項をチェックし、自分の受ける大学の数学の出題範囲を確認しておきましょう。
また、もしかすると勘違いしている人もいるかもしれませんが、理系学部の全てが理系数学を課すというわけではありません。 大学・学部によっては、理系学部でも文系数学を受けるようにとの指示があります。 例えば、看護学部なんかは文系数学で受験するパターンがとても多いです。 数学Cが苦手な理系学生は、色んな大学の入試情報をチェックし、文系数学で受験できる大学・学部の中から志望校を決めるという戦略も有りでしょう。
出題範囲を確認しておかないと、本来やらなくてもいいはずの範囲まで気付かずに学習してしまうということも起こり得るので、必ず事前に出題範囲を調べておきましょう。
③数学の定期テストで80点以上取るためには予習・復習を取り入れるべき

数学を苦手とする人は多いですが、中間テスト・期末テストの定期テストにおいてはテスト範囲が絞られますので、80点以上の高得点を狙うチャンスです。 定期テストで高得点が取れると、内申点UPにつながります。 また、自信が付きやる気も出ることにより、さらに勉強を頑張ろうとする良いサイクルができあがります。
数学や英語は積み上げ式だと言われるように、1年生の内容が2年生で習う内容にも絡んできますし、今日習ったことが明日の授業にもつながってきます。 よって、数学の定期テストで80点以上を取るためには、毎回の学校の授業を大切にし、その日のことはその日のうちに理解する習慣を付けないといけません。 丸暗記ではなく、“理解”することが大事です。 そこでポイントとなる勉強法は「予習・復習」です。
まずは“予習”です。 翌日の授業で習う教科書の範囲に目を通し、明日どのようなことを習うのかイメージを持っておきましょう。 翌日の授業において数学の先生が詳しく説明してくれますので、なにも予習をしなかった場合と比べて積極的に授業を聴こうという姿勢が生まれやすいです。 授業をちゃんと聴いていない生徒もたくさんいますので、授業をちゃんと聴くだけでもそれらの生徒と大きく差を付けることができます。
次に“復習”です。 予習をしていったことで授業の内容が理解しやすかったでしょうが、安心するのはまだ早いです。 今日の授業で習った内容は、帰宅後に復習をしましょう。 疲れて帰宅する日もあると思いますが、5分~10分でも構わないので教科書・ノートの内容を見直すなどしておきましょう。 そうすれば全く復習しなかった場合と比べて、理解が深まり忘れにくくなるはずです。
また、やはり授業中に先生が説明してくれた部分は定期テストに出ます。 そこでもう1つ大切となることが“ノートの取り方”です。 先生が黒板に板書した内容を写すことは大前提として、それに加えてメモを追記することがとても大事です。 先生も人間なので、特に生徒たちに伝えたい重要ポイントは強調して話してくれますし、優しい先生だと「ここテストに出るから!」と教えてくれることもあります。
授業をちゃんと聴いているだけでテストに出そうな部分が分かるわけなので、そういった先生が強調してくれたポイントをノートにメモしていきましょう。 汚い字でも良いので、「←ココ出る」や「◎」などのメモをしていきましょう。 そのノートをテスト直前に何回か見直し、「←ココ出る」のメモがある公式や定理を中心に修得していけば、数学の中間テスト・期末テストで高得点を取れる可能性は高まるはずです。
④教科書勉強法を徹底し、公式・定理・計算力を鍛えよう。教科書ガイドや青チャート式の落とし穴とは?

高校数学は中学数学と比べて格段に難しいので、闇雲に勉強していては高得点が取れません。 時間を掛けた割に成果にはつながらないという状況だけは避けたいので、やはり効率的な勉強法を身に付けて挑むべき科目です。
数学を勉強する上でまずやるべきことは、教科書内容を徹底的に理解すること。 教科書内容が理解できていない状態で問題集に手を出すと、分からない問題だらけでしょう。 また、基礎知識が足りなさすぎて、解説を読んでも解説すらイマイチ理解できないでしょう。
教科書内容が大体理解できている状態で問題集に取り組むと、解説を読んで全く意味が分からないということはないはずです。 分かる問題、分からない問題の選別も正しくできるので、効率よくスムーズに問題集を進めていくことができます。 よって、『教科書理解→問題集』という順番が大事です。
教科書を理解するとは、章末問題を解けるレベルまで達するということです。 例題で公式や定理のポイントをつかみ、練習問題で実践し、章末問題まで解ける力を付けましょう。 教科書を理解する際に教科書ガイドに頼る人もいるかと思いますが、教科書ガイドを見れば答えがすぐ分かってしまうので、分からない問題に対してじっくり考えるという部分がおろそかになりがちです。 じっくり考えるクセを付けないとその場しのぎの解決にしかならず、時間が経つとすぐに忘れてしまうので注意しましょう。
教科書が理解できたら、使いやすい問題集を1冊決めてやり込んでいきましょう。 色んな問題集に手を出すのではなく、1冊を複数回繰り返す方が力は付きます。 問題を解く際には、入試本番を常に意識して途中式・計算式もきちんと書くようにしましょう。 解答解説を読んで重要なポイントを見つけたら、ノートにメモしておくことをおすすめします。
さて、問題集を選択する際に青チャートを使用する人も多いかと思います。 なぜなら、高校で渡される問題集の中に青チャートが含まれているパターンが多いからです。 青チャートには多くの問題パターンが掲載されており、凄い問題集ではあります。 ただ実際に青チャートを使用してみて、問題の多さと難しさに挫折してしまう人も毎年少なからずいます。 では高偏差値の難関大学に入るためには、青チャートの問題パターンを全て解けるようにならないといけないのでしょうか。 決してそんなことはありません。
自分の段階に合った問題、つまりは教科書レベルの基礎・標準問題を1つ1つ習得していけば、共通テストで高得点は取れますし、難関大学にも合格することは十分可能です。 ドリームの教材は教科書レベルの基礎・標準問題を身に付けることに重きを置いていますので、問題集選びに不安がある方はぜひ一度お試しください。
ここまでの作業を高3の夏休みくらいまでに済ませておくことが理想的なスケジュールです。 秋以降は、自分の受ける大学の過去問を使った勉強を進めていきましょう。 例年同じような問題傾向を続けている大学も多いので、過去問こそ傾向を正確につかむための最高の問題集です。 過去問も1度やったらおしまいではなく、定期的に何度か反復して解いてみましょう。 余裕があれば、似た傾向を持つ他大学の過去問演習にも取り組んでみると良いです。
共通テストの過去問に取り組むのは12月からで問題ありません。 今まで行ってきた教科書重視の勉強が、共通テストにも効果的ですので。 ただ共通テストはマーク式ということもあり、マークシート問題への慣れは必要です。 ゆえに、12月以降は共通テストの過去問に取り組みマーク問題対策を重視しましょう。
⑤微分積分、確率、図形などの頻出分野は最優先で対策しよう!
高校数学では様々な分野を学習しますが、やはり大学によって頻出分野というのがあります。 頻出分野を中心に対策した方が効率良いのは間違いないので、必ず過去問分析を行っておきましょう。
共通テストや多くの大学の個別学力検査で、ほぼ毎年のように出題されている超頻出分野があります。 それは「微分積分」です。
微分積分は苦手な人も多いと思いますが、苦手なままだと非常にマズいです。 逆に微分積分を得意にすることができれば、かなり有利に大学受験を戦えることになります。 よってココには時間を多く費やして構わないので、必ず微分積分をマスターするというつもりで頑張りましょう。 まずはグラフの書き方、増減表の書き方から理解できるようにしたいですね。
その他の分野ですと、「確率、図形、整数、数列」なども頻出分野だと言えるので、微分積分に次いで対策する価値が高いでしょう。
⑥数学の入試問題に最適な問題集・参考書とは?

数学の入試問題を解く力を付けるにあたって最適なものは教科書です。 ほとんどの大学の入試問題に共通して言えることが、教科書の内容を参考に問題が作られており、教科書の内容を徹底的に理解することが合格点到達への一番の近道だということです。
そして、自分の受ける大学の過去問もとても重要です。 大学によって、校風も異なれば、どのような学生に入学してほしいかも異なり、それらの特徴が顕著に表れているのが入試問題です。 ゆえに、その大学の過去問にみっちり取り組んでいくことこそ、ベストな志望校対策となります。
ただ教科書というものは硬い文章で書かれているので、参考書の方が読みやすくて分かりやすいと感じる人もいるでしょう。 特に高校数学は学習する内容が複雑なものも多いので、噛み砕いた文章で説明をしてくれている参考書を1冊手元に置いておいた方が良いかもしれません。
また、ドリームには24時間視聴可能な解説動画もあります。数学の苦手分野に対して繰り返し何度も学習できる点が魅力です。
高校の数学で使用されている教科書の採択表はこちら
ドリームの数学対策は基本的に教科書に準拠した対応をさせていただいておりますが、一部対応できない教科書もありますのでご了承ください。ドリームでは学校の教科書の各単元で学ぶ内容の要点学習と、関連学習による大学受験勉強によって、授業対策と大学受験対策の日々の学習に効率的に取り組んでいくことができます。
数学Ⅰ
| 出版社 | 教科書 |
| 東京書籍 | 数学Ⅰ Advanced 数学Ⅰ Standard 数学Ⅰ Essence 新数学Ⅰ 新数学Ⅰ 解答編 |
| 実教出版 | 数学Ⅰ Progress 新編 数学Ⅰ 高校数学Ⅰ |
| 啓林館 | 数学Ⅰ 新編 数学Ⅰ 深進 数学Ⅰ |
| 数研出版 | 新編 数学Ⅰ 最新 数学Ⅰ 新 高校の数学Ⅰ NEXT 数学Ⅰ |
| 第一学習社 | 新編 数学Ⅰ 新編 数学Ⅰ サポートブック |
数学Ⅱ
| 出版社 | 教科書 |
| 東京書籍 | 数学Ⅱ Advanced 数学Ⅱ Standard 数学Ⅱ Essence 新数学Ⅱ 新数学Ⅱ 解答編 |
| 実教出版 | 数学Ⅱ Progress 新編 数学Ⅱ 高校数学Ⅱ |
| 啓林館 | 数学Ⅱ 新編 数学Ⅱ 深進 数学Ⅱ |
| 数研出版 | 新編 数学Ⅱ 最新 数学Ⅱ 新 高校の数学Ⅱ NEXT 数学Ⅱ |
| 第一学習社 | 新編 数学Ⅱ 新編 数学Ⅱ サポートブック |
数学Ⅲ
| 出版社 | 教科書 |
| 東京書籍 | 数学Ⅲ Advanced 数学Ⅲ Standard |
| 実教出版 | 数学Ⅲ Progress 新編 数学Ⅲ |
| 啓林館 | 数学Ⅲ 新編 数学Ⅲ 深進 数学Ⅲ |
| 数研出版 | 新編 数学Ⅲ 最新 数学Ⅲ 新 高校の数学Ⅲ NEXT 数学Ⅲ |
| 第一学習社 | 新編 数学Ⅲ |
数学A
| 出版社 | 教科書 |
| 東京書籍 | 数学A Advanced 数学A Standard 数学A Essence 新数学A 新数学A 解答編 |
| 実教出版 | 数学A Progress 新編 数学A 高校数学A |
| 啓林館 | 数学A 新編 数学A 深進 数学A |
| 数研出版 | 新編 数学A 最新 数学A 新 高校の数学A NEXT 数学A |
| 第一学習社 | 新編 数学A 新編 数学A サポートブック |
数学B
| 出版社 | 教科書 |
| 東京書籍 | 数学B Advanced 数学B Standard 数学B Essence |
| 実教出版 | 数学B Progress 新編 数学B 高校数学B |
| 啓林館 | 数学B 新編 数学B 深進 数学B |
| 数研出版 | 新編 数学B 最新 数学B 新 高校の数学B NEXT 数学B |
| 第一学習社 | 新編 数学B |
数学C
| 出版社 | 教科書 |
| 東京書籍 | 数学C Advanced 数学C Standard 数学C Essence |
| 実教出版 | 数学C Progress 新編 数学C 高校数学C |
| 啓林館 | 数学C 新編 数学C 深進 数学C |
| 数研出版 | 新編 数学C 最新 数学C 新 高校の数学C NEXT 数学C |
| 第一学習社 | 新編 数学C |
ドリームなら…
数学の質の高い予習・復習・テスト対策勉強をするのにピッタリの教材があります。
あなたのレベルに合った勉強ができる
ドリームは、あなたの学校の数学の教科書の要点にピッタリ対応した教材で、基礎問題から応用問題まで、詳しく分かりやすく解説します。
24時間いつでもみられる教材解説動画で、
あなたのペースで勉強できる
ドリームでは、教材の内容を1問1問解き方から詳しく解説した動画を24時間いつでもみることができます。
① 分からない問題だけピンポイントで学習できる
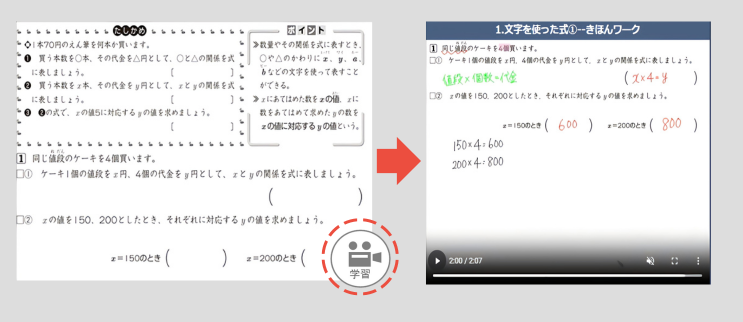
各単元の大問単位で動画が分かれているので、わからない部分があれば、その問題だけの動画解説を見ることができます。
また、数学なら途中式まで、英語なら文章構造までを詳しく解説しているので、動画をみるだけで解決できます。
② 同じ問題を繰り返し学習できる

予備校や塾の先生に説明してもらったけど理解できない時、「何度も同じ問題を聞き返すのが気まずい…」ということはありませんか?
塾の先生や家庭教師の先生には恥ずかしくて何度でも聞けないような問題でも、繰り返し何度でも学習することができるので、分からないところがそのままになるということがありません。
③ 学校の宿題のノートまとめも楽々!さらに、それがそのままテスト勉強になる
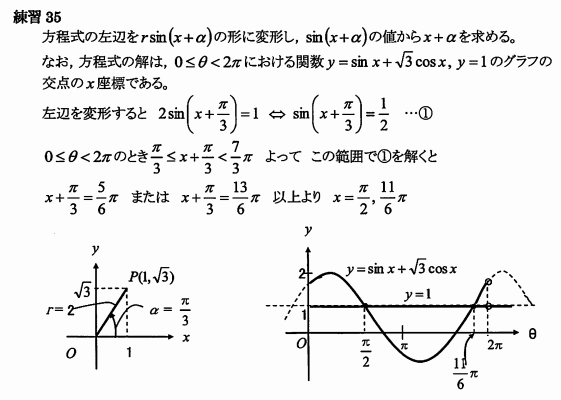

ドリームの映像解説動画では、教科書の重要ポイントを色分けして分かりやすく解説しています。
学校の定期テストは、今あなたが学校で使っている教科書からしか出題されません。
教科書の重要ポイントが分かっていれば、それを宿題の「自学ノート」に書き込んでいくことで、定期テストの勉強と宿題を同時にこなせて一石二鳥です。
さらに…
効率よく予習・復習・テスト対策ができる
① 問題の解き方から丁寧に解説

ドリームの教材は、学校の教科書で必ず理解しなければならないポイントを、分かりやすく、簡単にまとめてあります。
教科書の中で絶対に押さえるべき問題の解き方を、ステップに分けて詳しく解説するため、授業の予習がとってもラクになります。
② 定期テストに出る問題のパターンをおさえた、短時間でできる復習

ドリームの教材を使えば、復習も効率よく行えます。復習では、あなたの高校の教科書に合わせて、定期テストに出る問題のパターンをしっかりとおさえた問題に取り組めるので、無駄がなく短時間で復習することができ、しかもそれがそのままテスト対策にもつながります。












